На этой странице рассмотрен пример расчёта разбивочных элементов для некоторых из способов производства разбивочных работ. При этом принцип расчёта подробно пояснен, и его легко применить практически к любому другому способу.
Расчёт разбивочных элементов
Разбивочными элементами являются углы, расстояния, превышения, которые непосредственно строят на местности для получения проектного положения точек или линий сооружаемого объекта.
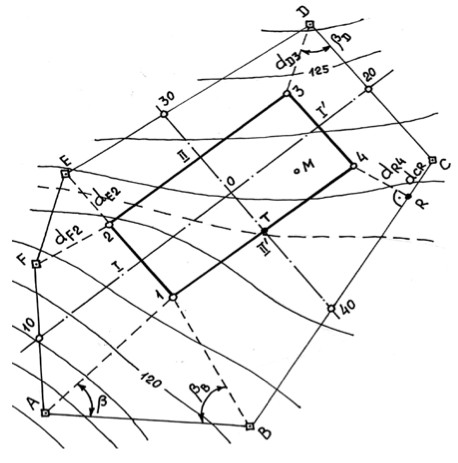
На местности имеется геодезическая основа А-В-С-D-E-F (см. рис.) с известными координатами Х, Y, H, заданными в местной системе координат (табл. 9.1). Необходимо вынести на местность углы 1, 2, 3 и 4 прямоугольного контура с размерами сторон d12= d34= 30,000 м и d23= d41 =75,000 м, а также выполнить разбивку главных осей I-I' и II-II' сооружения и передать проектную высоту на точку М.
С топографического плана (проекта сооружения) получены следующие проектные величины:
- координаты центра сооружения: ХО = 3730,000 м; YО = 7180,000 м;
- дирекционный угол направления главной оси I-I' α1 = 67030'.
Установлена проектная высота точки М НМ(ПР) = 123,600 м.
Таблица 9.1
| Пункты основы | Х, м | Y, м | Н, м |
|---|---|---|---|
| A | 3673,681 | 7112,241 | 117,403 |
| B | 3662,429 | 7166,522 | 120,352 |
| C | 3734,968 | 7237,400 | 123,363 |
| D | 3774,576 | 7217,639 | 126,050 |
| E | 3750,263 | 7132,405 | 122,901 |
| F | 3722,592 | 7121,946 | 120,600 |
При составлении геодезического проекта разбивочных работ с учётом взаимного расположения контура сооружения и геодезической основы принято следующее решение:
- точку 1 вынести способом прямой угловой засечки с точек А и В основы;
- точку 2 вынести способом линейной засечки с точек Е и F основы;
- точку 3 вынести способом полярных координат с точки D основы от исходного направления DC;
- главную ось симметрии I-I' зафиксировать в створе линий АF и DC в точках 10 и 20;
- главную ось симметрии II-II' зафиксировать в створе линий DE и ВС в точках 30 и 40;
- проектную высоту на точку М передать с точки С основы с контрольным определением построения проектной отметки через точку D.
Обратите внимание на то, что техническое задание на производство разбивочных работ здесь составлено условно, исключительно в учебных целях, с учётом рассмотрения возможно большего числа способов разбивки. Таким образом, представленный в примере проект разбивки для данного сооружения и данных условий может оказаться не оптимальным с точки зрения практического его воплощения.
Решение задачи в части определения величин разбивочных элементов.
Из решения обратных геодезических задач находим дирекционные углы и горизонтальные проложения исходных направлений геодезической основы (табл. 9.2).
Таблица 9.2
| Направление | Дирекционный угол | Горизонтальное проложение, м | Направление | Дирекционный угол | Горизонтальное проложение, м |
|---|---|---|---|---|---|
| АВ | 101o 42' 40" | 55,435 | DE | 254o 04' 45" | 88,634 |
| ВС | 44o 20' 11" | 101,418 | EF | 200o 42' 20" | 29,582 |
| CD | 333o 29' 05" | 44,264 | FA | 191o 13' 23" | 49,864 |
Найдем плановые координаты и высоты (на местности) проектных точек сооружения.
Часто координаты проектных точек получают непосредственно с плана графическим методом. Здесь мы рассмотрим аналитический, наиболее точный метод определения координат проектных точек.
В соответствии с геометрией сооружения и проектными исходными данными вычислим проектные значения прямоугольных координат углов сооружения (точек 1, 2, 3, и 4). Для этого воспользуемся вспомогательной точкой Т.
Дирекционный угол αОТ = α30-40 = α1 + 90о = 67о30' + 900 = 157о30'.
Горизонтаьное проложение dОТ = 0,5 d12 = 15,000 м.
Дирекционный угол αТ1 = α1 + 180о = 67о30' + 90о = 247о 30'.
Горизонтальное проложение dТ1 = 0,5 d23 = 37,500 м.
Найдем координаты точки 1 из последовательного решения прямых геодезических задач по ходу О-Т-1:
Х1 = ХО + dOT cos αOT + dT1 cos αT1 = 3701,791м
Y1 = YО + dOT sin αOT + dT1 sin αT1 = 7151,095м
Координаты остальных точек также определяем из решения прямых геодезических задач по ходу 1-2-3-4 с контрольным вычислением координат точки 1:
Х2 = X1 + d12 cos α12 = 3729,507м;........Y2 = Y1 + d12 sin α12 = 7139,614м
Х3 = X2 + d23 cos α23 = 3758,208м;........Y3 = Y2 + d23 sin α23 = 7208,905м
Х4 = X3 + d34 cos α34 = 3730,492м;........Y4 = Y3 + d34 sin α34 = 7220,386м
Х1 = X4 + d41 cos α41 = 3701,791м;........Y1 = Y4 + d41 sin α41 = 7151,095м
Для определения координат створных точек необходимо решить систему уравнений для двух пересекающихся линий. Например, для точки 10 пересекающиеся линии AF и О-10 имеют соответственно дирекционные углы αО-10 ==α1 +180о =67о30'+180о =247о30'; αAF =αFA +180о =11о13'23".
Можно записать следующие системы уравнений для координат Х и Y точки 10:
X10 = XО + dO−10 cos αO−10 = XA + dA−10 cos αAF ; (формула 9.19)
Y10 = YО + dO−10 sin αO−10 = YA + dA−10 sin αAF .
Из уравнений (9.19) выразим и вычислим значения неизвестных горизонтальных проложений:
dA-10 = (XO −XA) tg αO−10 −(YO −YA) / cos αAF tg αO−10 −sin αO−10 = 31,382м . (формула 9.20)
dO−10 = XA −XO + dA−10 cos αAF / cos αO−10 = 66,732м
По формулам (9.19) находим значения координат точки 10: Х10 = = 3704,463 м; Y10 = 7118,348 м.
Аналогичные уравнения составляют и для определения координат точек 20, 30 и 40.
В таблице 9.3 приведены проектные значения координат искомых точек, а также высоты этих точек, полученные с топографического плана.
Таблица 9.3
Проектные точки Х, м Y, м Н, м
10
3704,463
7118,348
119,05
20
3750,555
7229,624
124,55
30
3760,264
7167,465
124,40
40
3692,233
7195,644
122,10
1
3701,791
7151,095
121,30
2
3729,507
7139,614
121,90
3
3758,208
7208,905
124,65
4
3730,492
7220,386
123,35
М
Заданная проектная
высота
123,45
На этом заканчиваются подготовительные расчётные работы, после чего можно вычислить значения разбивочных элементов.
Вычисление разбивочных элементов для створных точек 10, 20, 30 и 40.
Каждую из указанных точек выносим на створ соответствующей линии с двух концов этой линии. Разбивочными элементами для выноса створных точек являются горизонтальные проложения d от исходных точек, а при практическом исполнении – наклонные расстояния s. Горизонтальные проложения находят из решения обратной геодезической задачи по координатам соответствующих точек. Например, для точки 10
dA-10 = √(XA - X10 )2 + (YA - Y10 )2 = 31,382м
dF-10 = √(XF - X10 )2 + (YF - Y10 )2 = 18,483м
Контроль: dA−10 + dF−10 = 49,865м = F−A (49,864 м; табл. 9.2), что допустимо.
Наклонные расстояния определяем по формулам
sA-10 = √d2A-10 + h2A-10 = 31,485м;……..sF-10 = √d2F-10 + h2F-10 = 18,548м, в которых
h10-A = H10 - HA = 119,05−117,40 = +1,65м;....h10−F = H10 − HF = −1,55м.
Аналогичные вычисления выполняют и для остальных створных точек (табл. 9.4).
| Проектные точки | Исходные точки | Горизонтальные проложения, | Превышения, м | Наклонные расстояния, м |
|---|---|---|---|---|
| 10 | A | 31,382 | +1,65 | 31,485 |
| F | 18,483 | -1,55 | 18,548 | |
| 20 | D | 26,845 | -1,50 | 26,887 |
| C | 17,419 | +1,20 | 17,460 | |
| 30 | E | 36,459 | +1,50 | 36,490 |
| D | 52,175 | -1,65 | 52,201 | |
| 40 | C | 59,748 | -1,25 | 59,761 |
| B | 41,670 | +1,75 | 41,707 |
При практическом построении створных точек, если требуется высокая точность построения проектных точек, вводят поправки за компарирование мерного прибора и поправки за температуру.
Вычисление разбивочных элементов для точек 1, 2, 3 и 4.
Точка 1. Выносится на местность способом прямой угловой засечки построением горизонтальных углов βА и βВ в точках А и В. Горизонтальные углы (разбивочные элементы) определяются как разность дирекционных углов соответствующих направлений:
βA = αАВ − αА1 ; βB = αВ1 − αBА . (формула 9.21)
Из решения обратной геодезической задачи
αА1 = 54о06'54"; αВ1 = 338о35'55".
Следовательно,
βА = 101о42'40" – 54о06'54" = 47о35'46"; βВ = 338о35'55" – 291о42'40" = 46о53'15".
Точка 2. выносится на местность способом линейной засечки с точек E и F расстояниями sE2 и sF2.
Из решения обратной геодезической задачи горизонтальные проложения dE2 = 21,972 м ; dF2 = 18,973 м. Превышения h2-E = -1,00 м; h2-F = +1,30 м. Следовательно, sE2 = 21,995 м и sF2 = 19,017 м.
Точка 3. Выносится на местность способом полярных координат с точки D от исходного направления DC (αDC = 153о29'05"). Разбивочными элементами являются горизонтальное проложение dD3 (наклонное расстояние sD3) линии D3 и горизонтальный угол в точке D (βD).
Из решения обратной геодезической задачи дирекционный угол αD3 = =208о05'04"; горизонтальное проложение dD3 = 18,552 м. Превышение h3-D = =124,65 – 126,05 = -1,40 м.
Горизонтальный угол βD = αD3 - αDC = 208о05'04" – 153о29'05" = 54о35'59". Наклонное расстояние sD3 = 18,605 м.
Точка 4. Выносится на местность способом прямоугольных координат наклонными отрезками sСR (по линии СВ) и sR4 (по перпендикуляру к линии СВ).
Горизонтальные проложения dСR и dR4 указанных отрезков найдем из решения системы уравнений
X4 = XC +dCR cos αCB + dR4 cos αR4 ,
Y4 = YC +dCR sin αCB + dR4 sin αR4 , (формула 9.22)
где αСВ = 224о 20'11"; αК4 =αСВ + 90о = 314о 20'11".
После подстановки в уравнения (9.22) всех известных величин получим dCR = 15,092 м , dR4 = 9,041 м.
С топографического плана получим высоту точки R HR = 122,90 м. Следовательно, hR-C = -0,45 м , h4-R = +0,45 м.
Наклонные расстояния sСR = 15,099 м, sR4 = 9,052 м.
После выноса на местность точек 1, 2, 3 и 4 выполняют контрольные промеры расстояний 1-2, 2-3, 3-4 и 4-1 с определением соответствующих горизонтальных проложений и сравнивают полученные значения с проектными. Кроме того, в точках 1, 2, 3 и 4 измеряют теодолитом проектные горизонтальные углы (90о). Контрольным измерением для прямоугольника является проверка длин его диагоналей 1-3 и 2-4, если прямоугольник располагается на выровненной площадке.
Точка М. Вынос точки на проектную высоту (123,45 м, табл. 9.3) осуществляется с точки С с контрольным определением её значения с исходной точки D.
Вычисляют проектное превышение hМ-С(ПР) = НМ(ПР) – НС = 123,450 – 123,357 = = + 0,093 м и контрольное проектное превышение hМ-D(ПР) = Н М(ПР) – НD = = 123,450 – 126,050 = - 2,600 м.
Нивелир устанавливают посредине между точками С и М и выполняют построение проектной отметки в соответствии с правилами, изложенными в геодезических работах при строительстве промышленных сооружений.
Аналогичные работы выполняют и при контрольной проверке построения проектной высоты с точки D. Однако здесь следует иметь в виду, что, скорее всего, с одной станции невозможно будет увидеть обе рейки, установленные в точках D и М, поскольку превышение между этими точками значительное, почти равно длине нивелирной рейки. В этом случае проверка построения высоты выполняется двумя станциями (ходом) через иксовую точку. Суммарное превышение (hx-D + hM-x) должно соответствовать проектному превышению hM-D(ПР).



